Die Mathematik des Floppy Cube
Diese Seite beschäftigt sich mit dem 1x3x3 Zauberwürfel, dem sogenannten Floppy Cube.

Notation
Die Züge am Floppy Cube werden mit F, R, L und B bezeichnet.
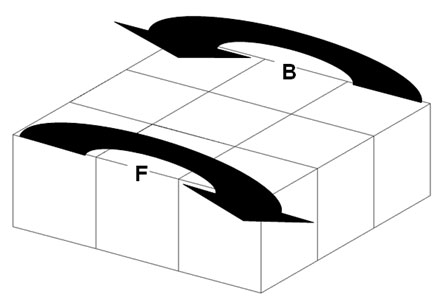
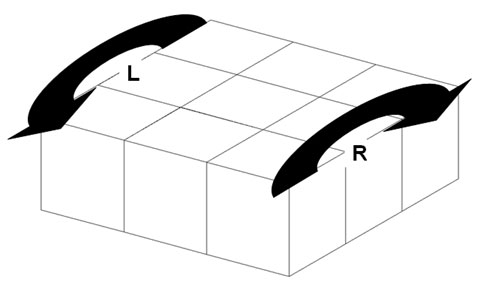
F^2 bedeutet, dass der Zug F zwei Mal durchgeführt wird und F^-1 bedeutet, dass der Zug F in die entgegengesetzte Richtung durchgeführt wird. Analog folgt die Bezeichnung für die übrigen Basiszüge.
Die Eck- und Kantenwürfel am Floppy Cube werden durchnummeriert.
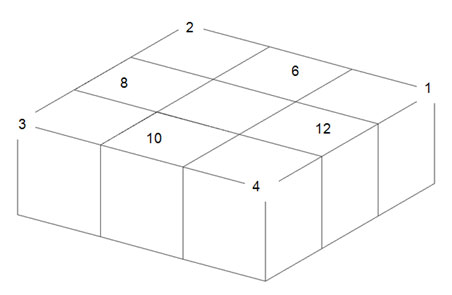
Tipps zum Lösen des Floppy Cube
Der Würfel in der Mitte des Floppy Cube gibt jeweils die Farbe für die obere und die untere Seite der kleinen Würfeln an und die Seitenflächen der Kantenwürfeln geben die Farben für die Seitenflächen der Eckwürfeln an!
Wie kann man die Eckwürfel an die richtige Position bringen? Durch Probieren kann man zuerst die Eckwürfel an die richtige Position bringen!
Wie kann man die Kantenwürfel richtig kippen? Mit dem Zug RBRBRB wird der rechte Kantenwürfel und der hintere Kantenwürfel gekippt.
Zulassungsarbeit
Alle Sätze und Details der Zulassungsarbeit können direkt in Kapitel 5 "Floppy Cube" ab Seite 30 inklusive aller Beweise nachgelesen werden. Die Zulassungsarbeit können Sie hier downloaden.
Die Mathematik des Floppy Cube
Mathematische Darstellung der Züge des Floppy Cube
Wie man beim Lösen des Floppy Cubes bereits entdeckt hat, kann man durch Züge am Floppy Cube nur die Position der Eckwürfel tauschen und die Kantenwürfel kippen.
1. Fall:
Die Permutation der Eckwürfel kann man wie beim Mini Cube durch Zykeln darstellen:
Beispiel: Zug RB mit der Zykeldarstellung (1 3 2) für die Permutation der Eckwürfel.
Satz:
Es gibt einen Homomorphismus \rho: G_Fl \rightarrow S_4, welcher jeden Zug am Floppy Cube auf seine Permutation der Eckwürfel abbildet.
2. Fall:
Das Kippen der Kantenwürfel kann ebenfalls durch Zykeln dargestellen werden:
Beispiel: Der Zug RB mit der Zykeldarstellung (5 6) (11 12) für das Kippen der Kantenwürfel.
Satz:
Es gibt einen Homomorphismus \sigma: G_Fl \rigtharrow S_2^4, welcher jeden Zug am Floppy Cube auf die Orientierung der Kantenwürfel abbildet.
3. Fall:
Indem die Zykeldarstellung der Permutation der Eckwürfel mit jener des Kippens der Kantenwürfel zusammengefügt wird, kann man so jeden Zug am Floppy Cube eindeutig beschreiben.
Beispiel: Der Zug RB wird mit der Permutationsdarstellung (1 3 2) (5 6) (11 12) beschrieben.
Satz:
Es gibt einen Homomorphismus \iota: G_Fl \rightarrow S_4 \times S_2^4, welcher jedem Zug die Permutation der Eckwürfel und die Orientierung der Kantenwürfel zuordnet.
Wiederholte Züge
Frage:
Erhält man irgendwann den gelösten Würfel, falls man einen Zug genug oft wiederholt?
1. Zug: RBRBRB
RBRBRB = (5 6) (11 12)
(RBRBRB)^2 = id.
2. Zug: RB
RB = (1 4 2) (5 6) (11 12)
(RB)^2 = (1 2 4)
(RB)^3 = (5 6) (11 12)
(RB)^4 = (1 4 2)
(RB)^5 = (1 2 4) (5 6) (11 12)
(RB)^6 = id
Resümee:
Um durch Wiederholung eines Zuges den gelösten Würfel zu erhalten, muss die Länge der verschiedenen Zykeln jeweils ein Faktor der Anzahl der Wiederholungen sein.
Die kleinste solche Zahl (das kleinste gemeinsame Vielfache von der Länge der verschiedenen Zykeln) heißt die Ordnung eines Zuges (oder Elements einer Gruppe).
Die Anzahl der Züge und endliche Präsentation des Floppy Cube
Alle Züge des Floppy Cube werden zusammengesetzt aus den Zügen F, B, R, L. Die Züge F,B, R, L werden jeweils durch zwei Transpositionen beschrieben und sind deshalb eine gerade Permutation. Da jeder Zug aus diesen geraden Permutationen aufgebaut ist, ist jeder Zug am Floppy Cube eine gerade Permutation. Würde jeder Eckwürfel die Position mit jedem anderen tauschen, so würde es maximal 4*3*2 = 24 verschiedene Möglichkeiten geben. Würde jeder Kantenwürfel gekippt werden würde es ingesamt 2^4 = 16 Möglichkeiten geben.
Insgesamt würde es also 16*24 Möglichkeiten geben, da es jedoch nur gerade Permutationen gibt, erhält man 192 verschiedene Züge am Floppy Cube.
Satz:
Es gibt insgesamt (4! * 2^4) / 2 = 192 verschiedene Züge am Floppy Cube.
Satz:
Es gilt G_Fl = < B, R, BLB, RFR | B^2 = R^2 = (BLB)^2 = (RFR)^2 = (LBLBL)^2 = (RLFLR)^2 = (RBRBR)^2 = (LFL)^2 = (FRF)^2 = (BRBRB)^2 = (BFLFB)^2 = (FRFRF)^2 = 1 >.
