Die Mathematik des Pocket Cube
Diese Seite beschäftigt sich mit dem 2x2x2 Zauberwürfel, dem sogenannten Pocket Cube.
(javascript-Applet ist lizensiert unter CC-3.0 und erstellt von W.Randelshofer)
Notation
Die Züge am Pocket Cube werden mit U, D, L, R, B und F bezeichnet.
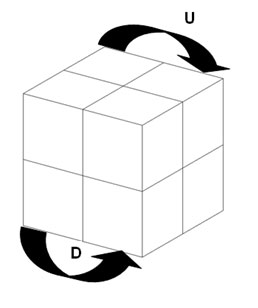
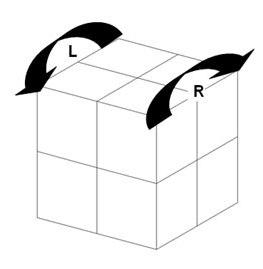
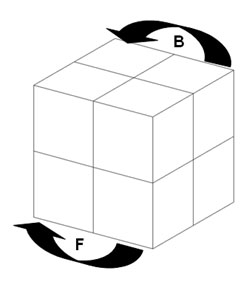
U^2 bedeutet, dass der Zug U zwei Mal durchgeführt wird und U^-1 bedeutet, dass der Zug U in die entgegengesetzte Richtung durchgeführt wird. Analog folgt die Bezeichnung für die übrigen Basiszüge.
Die Eckwürfel des Pocket Cubes werden durchnummeriert und mit Hilfe von Nummern werden die Züge dargestellt.
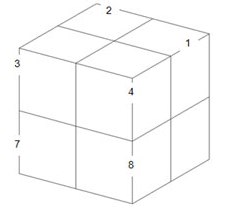
Tipps zum Lösen
Wie kann man die Eckwürfel an die richtige Position bringen? Der Zug FDF^-1D^-1R^-1D^-1R tauscht die Position des 7. Eckwürfels mit der des 8. Eckwürfels.
Wie kann man die Eckwürfel richtig orientieren? Der Zug R^-1D^-1RF^-1DR^-1DRD^2F^2 dreht den 6. Würfel im Uhrzeigersinn und den 7. Eckwürfel gegen den Uhrzeigersinn.
Mathematik kann zum Lösen des Pocket Cubes äußerst behilflich sein!
Zulassungsarbeit
Alle Sätze und Details der Zulassungsarbeit können direkt in Kapitel 6 "Pocket Cube" ab Seite 68 inklusive aller Beweise nachgelesen werden. Die Zulassungsarbeit können Sie hier downloaden.
Die Mathematik des Pocket Cube
Die Orientierung der Eckwürfel
In den Tipps zum Lösen des Pocket Cubes wurde bereits der Zug R^-1D^-1RF^-1DR^-1DRD^2F^2 angegeben, welcher den 7. und den 8. Eckwürfel dreht.
Indem man nun zwei beliebige Eckwürfel an die Position des 7. und des 8. Eckwürfels bringt, kann man diese beliebigen Eckwürfel ebenfalls drehen.
Beispiel:
Der Zug L^2 (R^-1D^-1RF^-1DR^-1DRD^2F^2) L^2 dreht den 3. und den 4. Eckwürfel.
Der Zug U^2L^2 (R^-1D^-1RF^-1DR^-1DRD^2F^2) L^2U^2 dreht den 1. und den 2. Eckwürfel.
Der Zug UL^2 (R^-1D^-1RF^-1DR^-1DRD^2F^2) L^2U dreht den 2. und 3. Eckwürfel.
Der Zug L^2 (R^-1D^-1RF^-1DR^-1DRD^2F^2) L^2 L^2U^2 (R^-1D^-1RF^-1DR^-1DRD^2F^2) U^2L^2 dreht den 1., 2., 3. und 4. Eckwürfel.
Der Zug U^2L^2 (R^-1D^-1RF^-1DR^-1DRD^2F^2) L^2U^2UL^2 (R^-1D^-1RF^-1DR^-1DRD^2F^2) L^2U dreht den 1., 2. und 3. Eckwürfel.
Satz:
Es gibt einen Homomorphismus \sigma: G_P \rightarrow C_3^8, welche jedem Zug die Orientierung der Eckwürfel zuordnet.
Beispiel:
\sigma(R^-1D^-1RF^-1DR^-1DRD^2F^2) = (0, 0, 0, 0, 0, 0, 1, 2)
Satz
Es gibt keinen Zug am Pocket Cube, welcher nur einen Eckwürfel dreht.
Die Permutationen der Eckwürfel
Beispiel:
Der Zug FDF^-1D^-1R^-1D^-1R vertauscht die Position des 7. Eckwürfels mit der des 8. Eckwürfels, jedoch wird auch der 6. Eckwürfel gedreht.
Nach obigen Überlegungen kann man jedoch bereits mittels Konjugation jenen Zug konstruieren, welcher nun die Orientierung von zwei beliebigen Eckwürfeln verändert.
Der Zug FDF^-1D^-1R^-1D^-1R vertauscht die Position des 7.Eckwürfels mit der des 8. Eckwürfels, jedoch wird auch der 6. Eckwürfel gedreht.
Wir haben allerdings jenen Zug bereits mittels Konjugation konstruiert, welcher nun die Orientierung von zwei beliebigen Eckwürfeln verändert.
Der Zug FDF^-1D^-1R^-1D^-1RR^-1D^-1RF^-1DR^-1DRD^2F^2 wird deshalb von der Permutation (7 8) beschrieben. Wie bereits oben gesehen kann man nun indem man zwei beliebige Eckwürfel an diese Position bringt, diese beiden Eckwürfel vertauschen.
Beispiel:
Der Zug R^2 (FDF^-1D^-1R^-1D^-1RR^-1D^-1RF^-1DR^-1DRD^2F^2) R^2 tauscht die Position des 1. Eckwürfels mit der des 7. Eckwürfels.
Der Zug U^2 (FDF^-1D^-1R^-1D-1RR^-1D^-1RF^-1DR^-1DRD^2F^2) U^2 tauscht die Position des 5. Eckwürfels mit der des 6. Eckwürfels.
Indem man diese Züge miteinander kombiniert, kann man beliebige Eckwürfel miteinander vertauschen.
Satz:
Es gibt einen Homomorphismus \rho: G_P \rightarrow S_8, welcher jeden Zug die Permutation der Eckwürfel zuordnet.
Beispiel:
\rho(FDF^-1D^-1R^-1D^-1RR^-1D^-1RF^-1DR^-1DRD^2F^2) = (7 8)
Eine mathematische Beschreibung der Züge des Pocket Cube
Bereits bei den Tipps zum Lösen des Pocket Cubes erkennt man, dass die Eckwürfel gedreht werden und die Position der Eckwürfel vertauscht werden kann, deshalb kann jeder Zug eindeutig durch seine Orientierung und seine Position beschrieben.
Satz:
Es gibt einen Homomorphismus \iota: G_P \rightarrow C_3^8 \rtimes S_8, welcher jedem Zug die Orientierung der Eckwürfel und die Permutation der Eckwürfel zuordnet.
Beispiel:
\iota(R^-1D^-1RF^-1DR^-1DRD^2F^2FDF^-1D^-1R^-1D^-1RR^-1D^-1RF^-1DR^-1DRD^2F^2) = ((0, 0, 0, 0, 0, 0, 1, 2,), (7 8))
Jedoch gibt es für das Element ((0, 1, 0, ..., 0), id) keinen Zug am Pocket Cube, welcher darauf abgebildet wird, da es keinen Zug am Pocket Cube gibt, welcher nur einen Eckwürfel dreht. Aber es gibt Züge, welche zwei oder drei Eckwürfel drehen, sodass folgt:
Satz:
Es gibt für ((w_1, ..., w_8), v) genau dann einen Zug am Pocket Cube, wenn w_1 + ... + w_8 = 0 (mod 3) ist.
Die Anzahl der Züge und endliche Präsentation des Pocket Cube
Zudem entspricht der Zug RL^-1 der Drehung R des gesamten Pocket Cubes. Da der Würfel 24 Drehungen besitzt, folgt aus obigen Überlegungen, dass die Anzahl der verschiedenen Züge bestimmt werden kann.
Satz:
Der Pocket Cube besitzt (8! * 3^7) / 24 = 3.674.160 verschiedene Züge.
Satz:
Es gilt G_P = < R, U, F | R^4 = F^4 = U^4; RURUR = URURU; UFUFU = FUFUF; RUFUR = UFURF; UFRFU = FRFRU; FRURF = URURF; (RF)^2(RU)^2(FU)^2 = 1 >.