An Introduction to Semirings

Semirings are generalised rings where negative elements do not have to exist. To be more precise, a semiring is a structure (R,+,*) such that (R,+) is a commutative semigroup, (R,*) is a semigroup and such that both distributive laws hold. We also assume the existence of a 0-element, which is neutral in (R,+) and absorbing in (R,*).

Every ring is also a semiring, and we call a semiring that is not a ring a proper semiring. A very prominent example of a proper semiring is the set of the natural numbers N={0,1,2,...} with their usual operations. But here we are interested mainly in finite semirings. The smallest example of a proper semiring with 1 is the so-called Boolean semiring:

    R2 = {0,1}
		    
    +  0 1     *  0 1 
		    
    0  0 1     0  0 0 
    1  1 1     1  0 1

The Boolean semiring is a semifield, i.e. all nonzero elements have a multiplicative inverse. Interestingly, it is the only finite proper semifield. Here is another example of a semiring with 1, with 6 elements (note that the element d is additively absorbing):

    R6 = {0,1,a,b,c,d}
		    
    +  0 a b c 1 d     *  0 a b c 1 d
		    
    0  0 a b c 1 d     0  0 0 0 0 0 0
    a  a a b c 1 d     a  0 0 0 a a b
    b  b b b 1 1 d     b  0 a b a b b
    c  c c 1 c 1 d     c  0 0 0 c c d
    1  1 1 1 1 1 d     1  0 a b c 1 d
    d  d d d d d d     d  0 c d c d d

The square matrices over a semiring form again a semiring. For example, the 2x2-matrices over the Boolean semiring result in the following semiring with 16 elements.

    R16 = {0,1,a,b,c,d,e,f,g,h,i,j,k,l,m,n}
		    
    +  0 a b c d e 1 f g h i j k l m n     *  0 a b c d e 1 f g h i j k l m n 
	    
    0  0 a b c d e 1 f g h i j k l m n     0  0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 
    a  a a c c e e f f h h j j l l n n     a  0 0 0 0 a a a a b b b b c c c c 
    b  b c b c 1 f 1 f i j i j m n m n     b  0 a b c 0 a b c 0 a b c 0 a b c 
    c  c c c c f f f f j j j j n n n n     c  0 a b c a a c c b c b c c c c c 
    d  d e 1 f d e 1 f k l m n k l m n     d  0 0 0 0 d d d d g g g g k k k k 
    e  e e f f e e f f l l n n l l n n     e  0 0 0 0 e e e e i i i i n n n n 
    1  1 f 1 f 1 f 1 f m n m n m n m n     1  0 a b c d e 1 f g h i j k l m n 
    f  f f f f f f f f n n n n n n n n     f  0 a b c e e f f i j i j n n n n 
    g  g h i j k l m n g h i j k l m n     g  0 d g k 0 d g k 0 d g k 0 d g k 
    h  h h j j l l n n h h j j l l n n     h  0 d g k a e h l b 1 i m c f j n 
    i  i j i j m n m n i j i j m n m n     i  0 e i n 0 e i n 0 e i n 0 e i n 
    j  j j j j n n n n j j j j n n n n     j  0 e i n a e j n b f i n c f j n 
    k  k l m n k l m n k l m n k l m n     k  0 d g k d d k k g k g k k k k k 
    l  l l n n l l n n l l n n l l n n     l  0 d g k e e l l i m i m n n n n 
    m  m n m n m n m n m n m n m n m n     m  0 e i n d e m n g l i n k l m n 
    n  n n n n n n n n n n n n n n n n     n  0 e i n e e n n i n i n n n n n

All semirings displayed so far are congruence-simple, which means that there is no nonzero homomorphism onto some smaller semiring. For rings, being congruence-simple is equivalent to being ideal-simple, and the Wedderburn-Artin-Theorem implies that the finite ideal-simple rings are exactly the matrix rings over finite fields.

Here is another congruence-simple semiring, which consists of 20 elements. It is in fact isomorphic to the endomorphism semiring of the monoid ({0,1,2,3},max).

R20 = {0,1,a,b,c,d,e,f,g,h,i,j,k,l,m,n,o,p,q,r}
		    
+  0 a b c d e f g h i j k l m 1 n o p q r    *  0 a b c d e f g h i j k l m 1 n o p q r 
		    
0  0 a b c d e f g h i j k l m 1 n o p q r    0  0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 
a  a a b c d e f g h i j k l m 1 n o p q r    a  0 0 0 0 0 0 0 0 0 0 a a a a a a b b b c 
b  b b b c e e f g h i k k l m 1 n o p q r    b  0 0 0 0 a a a b b c a a a b b c b b c c 
c  c c c c f f f h h i l l l 1 1 n p p q r    c  0 a b c a b c b c c a b c b c c b c c c 
d  d d e f d e f g h i j k l m 1 n o p q r    d  0 0 0 0 0 0 0 0 0 0 d d d d d d g g g i 
e  e e e f e e f g h i k k l m 1 n o p q r    e  0 0 0 0 a a a b b c d d d e e f g g h i 
f  f f f f f f f h h i l l l 1 1 n p p q r    f  0 a b c a b c b c c d e f e f f g h h i 
g  g g g h g g h g h i m m 1 m 1 n o p q r    g  0 0 0 0 d d d g g i d d d g g i g g i i 
h  h h h h h h h h h i 1 1 1 1 1 n p p q r    h  0 a b c d e f g h i d e f g h i g h i i 
i  i i i i i i i i i i n n n n n n q q q r    i  0 d g i d g i g i i d g i g i i g i i i 
j  j j k l j k l m 1 n j k l m 1 n o p q r    j  0 0 0 0 0 0 0 0 0 0 j j j j j j o o o r 
k  k k k l k k l m 1 n k k l m 1 n o p q r    k  0 0 0 0 a a a b b c j j j k k l o o p r 
l  l l l l l l l 1 1 n l l l 1 1 n p p q r    l  0 a b c a b c b c c j k l k l l o p p r 
m  m m m 1 m m 1 m 1 n m m 1 m 1 n o p q r    m  0 0 0 0 d d d g g i j j j m m n o o q r 
1  1 1 1 1 1 1 1 1 1 n 1 1 1 1 1 n p p q r    1  0 a b c d e f g h i j k l m 1 n o p q r 
n  n n n n n n n n n n n n n n n n q q q r    n  0 d g i d g i g i i j m n m n n o q q r 
o  o o o p o o p o p q o o p o p q o p q r    o  0 0 0 0 j j j o o r j j j o o r o o r r 
p  p p p p p p p p p q p p p p p q p p q r    p  0 a b c j k l o p r j k l o p r o p r r 
q  q q q q q q q q q q q q q q q q q q q r    q  0 d g i j m n o q r j m n o q r o q r r 
r  r r r r r r r r r r r r r r r r r r r r    r  0 j o r j o r o r r j o r o r r o r r r

These are in fact the smallest congruence-simple proper semirings, together with another semiring: the zero-multiplication ring of size 2. The next semiring in the row has already 42 elements. Despite of this sparsity of congruence-simple semirings, there are plenty of general semirings, as can be seen in the following table.

                    all        congruence-simple
    size   semirings   rings    semirings rings
		    
      2            4      2          4       2
      3           22      2          2       2
      4          283     11          1       1
      5        4'717      2          2       2
      6      108'992      4          1       0
      7    8'925'672      2          2       2
    2...7  9'039'691     23         12       9

A classification of all finite proper congruence-simple semirings can be given with the help of lattices.

Lattices and Semirings

A lattice is an ordered set (L,≤) in which every pair of elements has both a supremum and an infimum in L. They can be depicted by order diagrams, which show only the covering pairs (y covers x iff x<y and there is no z with x<z<y).

The supremum operation converts the lattice into a commutative idempotent semigroup, which is in the finite case even a monoid. Conversely, every commutative idempotent monoid (L,+) gives rise to an ordered set (L,≤) by defining x≤y iff x+y=y, which turns out to be a lattice.

Let L be a lattice with supremum operation ∨. Then the endomorphisms End(L,∨) of the monoid (L,∨) is naturally a semiring, and these semirings are congruence-simple. On the other hand, the following statement can be proven (see arXiv:math/0702416):

Theorem. Let R be a finite proper congruence-simple semiring with nonzero multiplication. Then R is isomorphic to a 'dense' subsemiring S of the endomorphism semiring End(L,∨) of some lattice L. (Here, a subsemiring S⊆End(L,∨) is called 'dense' if every endomorphism f∊End(L,∨) with |Im f|≤2 is contained in S.)

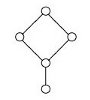
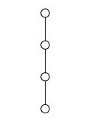
The following table displays the diagrams of the smallest lattices (with at least 2 elements) together with the corresponding congruence-simple semirings, according to the above theorem. We write R_n for a semiring with n elements.

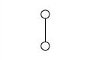The smallest lattices along with the corresponding congruence-simple semirings.
	R₂ (the Boolean semiring)
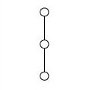	R₆
	R₂₀ (the 2x2-matrices over R₂)
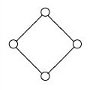	R₁₆
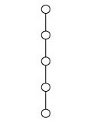	R₇₀
	R_50,a
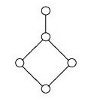	R_50,b
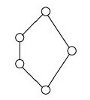	R₄₃, R₄₂
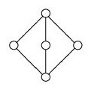	R_50,c, R₄₇, R_46,a, R_46,b, R_46,c R₄₅, R₄₄ (where R_46,a,R_46,b,R_46,c are isomorphic)

One can also prove that a lattice L corresponds to only one congruence-simple semiring (namely its full endomorphism semiring End(L,∨)) if and only if the lattice L is distributive.

An Introduction to Semirings

Lattices and Semirings

Further Reading