Komplexe Zahlen

Was sind komplexe Zahlen? oder: Ein kleiner Ausflug in die "Fantasien" der Mathematiker

Schon im Mittelalter empfanden einige Mathematiker den Umstand als unbefriedigend, dass es keine Zahlen gibt, deren Quadrat negativ ist, und dass damit viele Gleichungen keine Lösungen haben - bis sie später solche Zahlen einfach erfanden. Genauer gesagt, bezeichneten sie mit der imaginären Einheit i eine Zahl, deren Quadrat -1 ergibt, und rechneten mit dieser wie gewohnt weiter (dabei geht man dann mit i um wie mit einer Variable, etwa x).

Sie stellten fest, dass mit Hilfe dieser Zahl viele Gleichungen jetzt Lösungen besitzen, die vorher nicht lösbar waren (sogar alle Polynomgleichungen haben jetzt eine Lösung!).
Ein Beispiel dazu: x² - 4 x + 5 = 0, umgeformt zu (x - 2)² = -1.
Früher: Wurzel ziehen unmöglich, wegen der rechten Seite (-1).
Jetzt: Wegen -1 = i² können wir die Wurzel ziehen: x - 2 = i oder x - 2 = -i. Als Lösungen ergeben sich also die Zahlen 2 + i und 2 - i.

Diese zusammengesetzten Zahlen, wie z.B. 2 + i, bestehen aus einem Realteil (2) und einem Imaginärteil (i, bzw. 1i). Aus Real- und Imaginärteil zusammengesetzte Zahlen nennt man auch komplexe Zahlen, darstellbar in der Form z = a + bi.

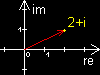Um sich komplexe Zahlen doch wiederum vorstellen zu können, kann man sie als Punkt in einer Ebene mit einer realen und einer imaginären Achse, der sog. Gauß'schen Zahlenebene darstellen. Die Skizze zeigt die Zahl 2 + i und einen Pfeil (oder Vektor) vom Ursprung zu 2 + i.

Die Grundrechenarten Addition und Multiplikation lassen sich einfach herleiten:

Addition

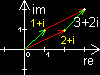z₁ + z₂ = a₁ + b₁i + a₂ + b₂i = a₁ + a₂ + (b₁ + b₂)i

Bsp.: z₁ + z₂ = 2 + i + 1 + i = 2 + 1 + (1 + 1)i = 3 + 2i

In der Gauß-Ebene ergibt sich die Addition durch das Hintereinanderlegen der Pfeile.

Multiplikation

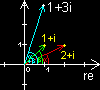z₁ · z₂ = (a₁ + b₁i) · (a₂ + b₂i)
= a₁a₂ + a₁b₂i + b₁ia₂ + b₁b₂i²
= a₁a₂ - b₁b₂ + (a₁b₂ + b₁a₂)i

Bsp.: z₁ · z₂ = (2 + i) · (1 + i) = 2 + 2i + i + i² = 1 + 3i

In der Gauß-Ebene ergibt sich die Multiplikation interessanterweise durch die Multiplikation der Pfeillängen und durch Addition der Pfeilwinkel bzgl. der realen Achse. Die Quadrierung ergibt sich ensprechend durch Quadrierung der Pfeillängen und der Verdoppelung des Pfeilwinkels.