IFS - Fraktale in der Natur

  

Für die nachfolgenden Fraktale verwenden wir, anders als bei der von Koch'schen Kurve oder beim Sierpinski-Dreieck, nicht nur reine Ähnlichkeitsabbildungen, sondern die allgemeineren affine Abbildungen. Erlaubt sind hier neben Verschiebung, Drehung und Verkleinerung auch X- und Y-Skalierung (unabhängig voneinander), Spiegelung und Scherung. Mehrere solcher Abbildungen zusammen nennt man auch Funktionssystem.

Barnsley-Farn

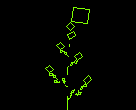
Beim Barnsley-Farn (nach Michael F. Barnsley) verwendet man ein Funktionssystem aus vier affinen Abbildungen. Das Funktionssystem wird auf ein Anfangsbild mehrmals angewandt und heißt daher iteriertes Funktionssystem (IFS). Im folgenden Beisipel besteht das Anfangsbild aus einem Quadrat.

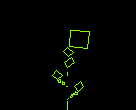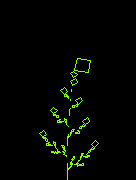Man beachte, dass eine Abbildung zu einer Linie ausgeeartet ist (X-Skalierung mit Faktor 0), die später den Zweig des Blattes darstellt. In der Bildergalerie gibt es ein großes Bild, das den Schritt 50 darstellt. Das Bild hat verblüffende Ähnlichkeit mit einem natürlichen Farn. Wir sehen also, dass sich scheinbar komplexe Strukturen, wie sie in der Natur vorkommen, mit nur wenigen Formeln beschreiben lassen (siehe die IFS-Koeffizienten).

Drachenkurve

Die Drachenkurve resultiert aus einem sehr einfachen IFS mit nur zwei Ähnlichkeitsabbildungen. Diese verkleinern das Ursprungsbild um den Faktor 1/√2 und sind um 45° bzw. 225° (gegen den Uhrzeigersinn) gedreht. Im folgenden Beispiel besteht das Anfangsbild wieder aus einem Quadrat, so dass auch alle weiteren Bilder aus Quadraten bestehen.

Interessant ist hier, dass der Flächeninhalt immer gleich bleibt, da der Flächeninhalt der jeweils zwei abgebildeten Quadrate je genau die Hälfte des vorigen Quadrats beträgt. Da sowohl die Quadrate als auch die Zwischenräume immer kleiner werden, entsteht ein "unendlich feines Netz", dessen "Flächeninhalt" gerade das doppelte des ursprünglichen Quadrats beträgt. Und so sieht die Kurve nach 50 Schritten aus:

Verwendet man anstatt eines Quadrates eine Strecke als Ausgangsbild, kann man die Entstehung des Fraktals noch etwas besser verfolgen: Bei jedem Schritt bilden Anfang und Ende aller Strecken die Mittelpunkte neuer Strecken, die um 45° im Uhrzeigersinn gedreht sind.

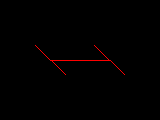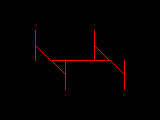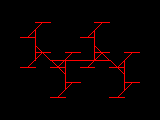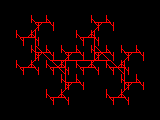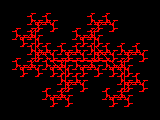Wir sehen, dass das Grenzbild stets die gleiche Form aufweist, egal ob wir mit einem Quadrat oder mit einer Strecke als Ursprungsbild starten. In der Tat hängt das Grenzbild eines IFS nicht vom Startbild ab (nach dem sog. Banach'schen Fixpunktprinzip) und man nennt das Grenzbild deswegen auch einen Attraktor (lat. abstrahere - anziehen). Die Grenzmenge verhält sich aber nur dann als Attraktor, wenn das IFS kontrahierend ist, d. h., anschaulich gesprochen, dass die abgebildeten Bilder jeweils "kleiner" sind als das Original, wie es beim Barnsley-Farn und der Drachenkurve der Fall ist.

Wer die Drachenkurve noch einmal etwas schöner dargestellt sehen will und durch weitere (auch dreidimensionale) IFS-Beispiele einen Eindruck gewinnen möchte, was mit IFS alles realisierbar ist, dem sei die Bilder-Galerie empfohlen.