Jens Zumbrägel's Website
Mathematics and More |
Farbdarstellungen komplexer Fraktale
 Stellt man nur die Mandelbrot-Menge bzw. die Julia-Menge
dar, benötigt man nur zwei Farben (Beispiel
links). Möchte man jedoch ein schöneres
Bild haben, kann man die Farbanzahl erhöhen und
jeden Punkt nach dem Verhalten der entsprechenden
Iteration einfärben. Die Farbe wird einer Farbskala
entnommen, dessen Index (Farbindex) eine positive ganze
Zahl ist, die sich aus der Iteration ergibt.
Stellt man nur die Mandelbrot-Menge bzw. die Julia-Menge
dar, benötigt man nur zwei Farben (Beispiel
links). Möchte man jedoch ein schöneres
Bild haben, kann man die Farbanzahl erhöhen und
jeden Punkt nach dem Verhalten der entsprechenden
Iteration einfärben. Die Farbe wird einer Farbskala
entnommen, dessen Index (Farbindex) eine positive ganze
Zahl ist, die sich aus der Iteration ergibt.
Mir sind drei Ansätze eingefallen, wie man den Farbindex bestimmen kann. (Auch wenn auf diesen Seiten relativ oft auf diese Farbdarstellungsformen verwiesen wird, möchte ich darauf hinweisen, dass sie keine geläufigen Begriffe in der Literatur sind.)
Erste Farbdarstellungsform
Farbindex = Anzahl Schritte bis Betrag größer als 2
In Flohsprache: Der Farbindex ist die Anzahl der Sprünge, die der Floh machen kann, bis er vom Tisch fällt.

Hier wurde pro Punkt maximal 100mal der Flohsprung verfolgt (Iterationstiefe 100). Die Mandelbrot-Menge (der Floh bleibt immer auf dem Tisch) ist schwarz dargestellt. Die meisten Fraktal-Bilder sind nach diesem Verfahren erstellt worden. Es ist auch am einfachsten zu programmieren.
Zweite Farbdarstellungsform
Farbindex = Anzahl Häufungspunkte
Bei den Flöhen, die immer auf dem Tisch bleiben, nähern sich viele Flöhe einem bestimmten Punkt an und springen immer auf dieser Stelle. Andere springen mit der Zeit zwischen zwei Punkten hin und her, einige wenige pendeln sogar zwischen drei oder mehr (endlich vielen) Punkten. Diese Punkte werden Häufungspunkte genannt.
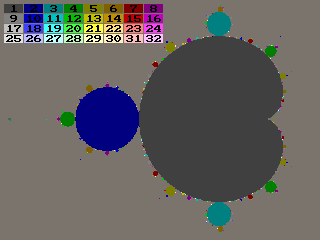
Iterationstiefe: 1000, maximale Anzahl der Häufungspunkte: 32
Man sieht, dass ein Bereich mit gleich vielen Häufungspunkten fast stets kreisförmig ist. Ferner sind Bereiche mit vielen Häufungspunkten viel kleiner als Bereiche mit wenig Häufungspunkten, dafür gibt es aber auch mehr solche Bereiche.
Dritte Farbdarstellungsform
Farbindex = Anzahl Schritte bis "feste" Pendelfolge erreicht
Wir wissen jetzt, dass sich Flöhe, die auf dem Tisch bleiben, sich einem Punkt oder mehreren Punkten annähern. Sie nähern sich aber unterschiedlich "schnell" diesen Punkten an. Wir wollen jetzt die Schritte zählen, die der Floh braucht, bis er eine bestimmten Nähe zu seinen Häufungstpunkten hat, so dass sich die Position kaum noch ändert, bzw. sich die Positionen bei der Pendelfolge jeweils kaum noch ändern. Im folgenden Beispiel springen die Flöhe solange, bis sich ihre Positionen um höchstens 0,001 änderrn.
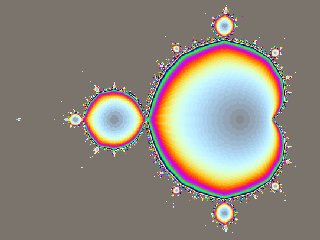
Iterationstiefe: 1000, Toleranzschwelle: 0,001
Man sieht, dass Flöhe in den Randbereichen der Menge sich nur langsam ihren Häufungspunkten annähern.
 |
© 2014 by Jens Zumbrägel |