Was sind Fraktale?

  

Als ein Fraktal bezeichnet man eine Punktmenge, die als "Grenzmenge" einer geeigneten Folge (M_n) von Punktmengen M₁, M₂, M₃, ... entsteht. Eine Punktmenge kann dabei aus einzelnen Punkten, Linien, Flächen oder Körpern bestehen.

Die Grenzmenge hat die Eigenschaft, dass sie sich bei beliebiger Vergrößerung "unendlich oft ändert".

von Koch'sche Kurve

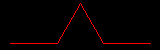
Oft kann man die Folge der Punktmenge rekursiv beschreiben, wie in unserem ersten Beispiel, der von Koch'schen Kurve (nach Helge von Koch, 1870-1924, schwed. Mathematiker):

Bei der von Koch'schen Kurve erzeugt man die Punktmenge M_n+1 aus M_n, indem man das mittlere Drittel jeder Strecke in M_n durch zwei Schenkel eines gleichseitigen Dreiecks ersetzt. Deutlich zu sehen ist hier die Selbstähnlichkeit dieses Fraktals, dass also in den nachfolgenden Fraktalen fortwährend die Grundform verkleinert (rechts grau eingefärbt) auftritt. Nachfolgend sind die ersten fünf Iterationsschritte dieser Folge und die entsprechenden Längen der Kurven dargestellt (Einheit willkürlich).

Zwei Dinge sind an dieser Folge von Punktmengen erwähnenswert:

• Die Kurve erinnert vor allem bei größeren Indizes an eine natürliche Figur, etwa an eine Schneeflocke. Es ist uns also gelungen, eine komplexe Figur durch eine sehr einfache Rekursionsvorschrift darzustellen.
• Außerdem wächst die Länge der Kurve M_n mit steigendem Index ins "Unendliche", obwohl sie in einem beschränkten Flächenstück liegt.

Wir können schwer sagen, ob die Grenzmenge eine Linie oder eine Fläche ist, also ob es sich um ein ein- oder ein zweidimensionales Gebilde handelt. Da man mit dem traditionellen Dimensionsbegriff nicht weiter kommt, spricht man auch von gebrochenen oder "fraktalen" (frangere - lat. zerbrechen) Dimensionen bzw. kurz "Fraktalen".

Sierpinski'scher Flickenteppich

Ein weiteres bekanntes Fraktal, welches auf Selbstähnlickeit beruht, ist der Sierpinski'sche Flickenteppich, auch Sierpinski-Dreieck genannt (nach Wacłlaw Sierpiński, 1882-1969, poln. Mathematiker). Es entsteht, wenn man, ausgehend von einem einzelnen Dreieck, bei jedem Schritt aus den vorhandenen Dreiecken jeweils ein kleineres Dreieck ausschneidet. Die Zahl der Dreiecke steigt dabei um das Dreifache.