"Komplexe" Fraktale

 

Die wohl bekanntesten Vertreter der Fraktale, das Mandelbrot- (oder Apfelmännchen) und Julia-Fraktal, resultieren nicht, wie die bisher besprochenen Fraktale aus (Ähnlichkeits- oder affinen) Abbildungen, sondern sind völlig anders aufgebaut. Leider ist die Erklärung dieser Fraktale auch nicht so einfach, doch es lohnt sich schon, sich mit ihnen auseinander zu setzen.

Sie resultieren aus einer einzigen Folge, welche rekursiv dargestellt ist:

Sieht doch ganz simpel und gar nicht "komplex", oder? - Der Haken ist jedoch, dass die Zahlen z_n und c eben komplex sind. Was komplexe Zahlen sind? Hier ein kurzer Ausflug in die Welt der komplexen Zahlen.

Mandelbrot-Fraktal

Wer sich mit den komplexen Zahlen nicht so recht anfreunden konnte, für den habe ich eine recht witzige und gut verständliche Erklärung für die Entstehung des Mandelbrot-Fraktals (nach Benoît Mandelbrot, 1924-2010, frz./US-Mathematiker), die ich aus einer Fernsehsendung übernommen habe:

Vor kurzem ist es durch die Genforschung geglückt, eine besondere Art von Flöhen zu züchten, die wohl große Mathe-Fans sind, was sich durch ihre besondere Sprungtechnik bemerkbar macht:

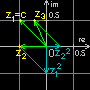Setzt man innerhalb der Gauß'schen Zahlenebene einen Floh (Position z₁, im Beispiel -0,5 + 0,5i) auf einen runden Tisch (Radius 2, Mittelpunkt im Ursprung), merkt er sich zunächst seine relative Position zum Ursprung (c). Mit jedem Schritt n springt der Floh (Pos. z_n) so, dass sein Abstand vom Ursprung das Quadrat des alten Abstands ist, und sich der Winkel, den Floh, Ursprung und X-Achse bilden, verdoppelt (z_n²). Anschließend springt er zur Seite, und zwar um die gemerkte Position (c) relativ zum jetzigen Standpunkt (z_n² + c).

Setzt man nun Flöhe an verschiedenen Stellen auf dem Tisch aus, fallen viele nach einem oder mehreren (endlich vielen) Schritten vom Tisch, und einige bleiben beim Springen immer auf dem Tisch.

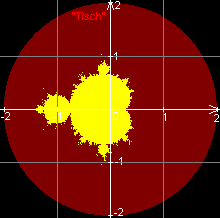
Färbt man nun alle Punkte gelb ein, von denen man aus Flöhe aussetzen kann, die immer auf dem Tisch bleiben, ergibt sich das Muster, was rechts zu sehen ist.

Die Menge aller gefärbten Punkte (bzw. der markierten komplexen Zahlen) stellt die wohl komplizierteste Menge der Mathematik dar, was sich hier am ungleichmäßen Umriss andeutet. Sie hat dafür sogar einen Eintrag im Guiness Buch der Rekorde bekommen. Man spricht deswegen oft von der Mandelbrot-Menge statt vom Mandelbrot-Fraktal.

Für die, die es etwas formaler wollen: Als Mandelbrot-Menge bezeichnet man die Menge aller komplexen Zahlen c, für die die komplexe Iteration z_n+1 = z_n² + c mit z₀ = 0 beschränkt ist. Mit z₀ = 0 ergibt sich z₁ = c, wie es im Floh-Beispiel erklärt ist. Bei dieser Iteration ist es so, dass sie bereits dann nicht beschränkt ist, wenn ein Element einen Betrag von mehr als 2 erreicht, also im Floh-Beispiel der entsprechende Floh vom Tisch fällt.

Wie man die Mandelbrot-Menge schön farblich darstellen kann, wird im Exkurs Farbdarstellungsformen erklärt.

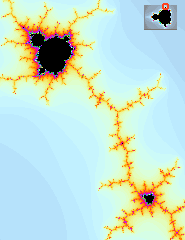
Eine Vorstellung von der Komplexität und Schönheit der Menge bekommt man vor allem, wenn man einzelne Bereiche der Menge vergrößert. Eine Kostprobe:

Der rote Kreis im kleinen Icon, was oben im Bild zu sehen ist, bezeichnet die Position in die hineingezoomt wurde. Im ersten Bild ist gut die Selbstähnlichkeit des Fraktals zu erkennen: Es treten unzählig viele kleine Abbilder des Apfelmännchens auf. Im zweiten Bild sieht man, dass das Fraktal auch Formen beinhaltet, die überhaupt nicht an das Apfelmännchen erinnern. Eine Fülle weiterer Bilder gibt es natürlich in der Bilder-Galerie.

Julia-Fraktal

Das Julia-Fraktal (nach Gaston Maurice Julia, 1893-1978, frz. Mathematiker) verwendet die gleiche Iterationsvorschrift, wie das Mandelbrot-Fraktal, nämlich z_n+1 = z_n² + c, nur bleibt hier die komplexe Zahl c stets konstant. Dafür ist jetzt der Startwert z₀ das Interessante.

Die Definition der Julia-Menge: Als Julia-Menge bezeichnet man die Menge aller komplexen Startzahlen z₀, für die die komplexe Iteration z_n+1 = z_n² + c beschränkt ist.

Um beim Flohbeispiel zu bleiben: Die Julia-Flöhe springen zunächst wie die Mandelbrot-Flöhe, nämlich so, dass der Floh (Pos. z_n) seinen Abstand vom Ursprung das Quadrat des alten Abstands ist, und sich der Winkel, den Floh, Ursprung und X-Achse bilden, verdoppelt (z_n²). Anschließend springt er zur Seite, und zwar um eine bestimmte Position c, die hier unabhängig vom Aussetzpunkt ist (z_n² + c).

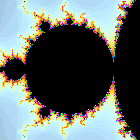
Im Unterschied zum Mandelbrot-Fraktal lässt sich also die Zahl c frei wählen, d. h. es lassen sich unendlich viele verschiedene Fraktale erzeugen. In den folgenden drei Beispielen ist neben den Julia-Fraktalen jeweils ein vergrößerter Mandelbrot-Ausschnitt zu sehen, der den Punkt c enthält. Der Farbindex entspricht der Anzahl Schritte bis der Betrag größer als 2 ist (Farbdarstellung 1), die Julia-Menge (schwarz dargestellt) ist nur im ersten Beispiel nicht leer.

Man erkennt eine gewisse Ähnlichkeit der Fraktale (wie man schon wegen der gleichen Rekursionsvorschrift vermuten könnte). So ist die Julia-Menge auch nur dann nicht leer, wenn c in der Mandelbrotmenge ist, wie im ersten Beispiel. Die Mandelbrot-Menge ist also in gewisser Hinsicht komplexer und interessanter als die Julia-Menge, weil in einer Iteration praktisch alle Formen der Julia-Mengen bereits enthalten sind. Vergrößert man eine Julia-Menge, kann man dagegen nicht so viele interessante und neue Formen entdecken. Dafür ist hier die Selbstähnlichkeit stärker ausgeprägt.

Für die farbige Darstellung der Julia-Menge kann man die gleichen Verfahren wie für die Mandelbrot-Mengen verwenden (hier werden sie erklärt). Nur ist die Farbdarstellungsform 2 (Farbindex = Anzahl Häufungspunkte) nicht sinnvoll, weil die Anzahl der Häufungspunkte bei allen Punkten der Julia-Menge gleich der Anzahl ist, die sich in der Mandelbrotmenge mit Startpunkt c ergibt. Die beiden anderen Methoden liefern aber schöne Bilder, welche in der Bilder-Galerie zu finden sind.