Bildergalerie

IFS-Bilder · IFS-3D-Bilder · Mandelbrot-Fraktale · Julia-Fraktale

Mandelbrot-Fraktale

Zu diesen Bildern

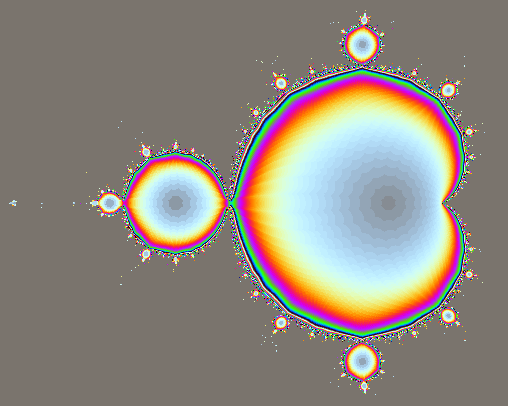
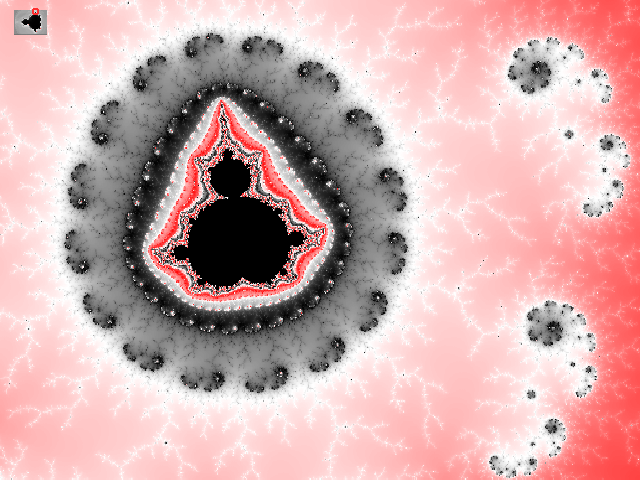
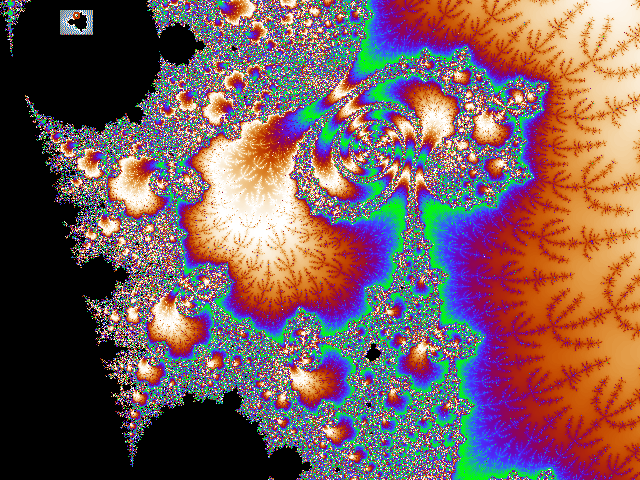
Wie das Mandelbrot-Fraktal entsteht wird im Kapitel komplexe Fraktale erklärt. Die Formeln gibt es hier, so dass die Programmierung eigentlich kein Problem darstellt. Es wurden für die einzelnen Bilder unterschiedliche Farbskalen verwendet.

Die ersten drei Bilder zeigen drei mögliche Farbdarstellungen der Mandelbrot-Iteration.

Die nächsten sechs Bilder zeigen verschiedene, stark vergößerte Ausschnitte aus dem Mandelbrot-Fraktal (in erster Farbdarstellung). Das kleine Mandelbrot-Icon, was in jedem der Zoom-Bilder auftaucht, gibt den Punkt an, in den hineingezoomt wurde. Der Vergrößerungsfaktor (im Vergleich zu den ersten drei Bildern) und die Iterationstiefe der jeweiligen Bilder ist wie folgt:

Bild 1 2 3 4 5 6

Zoomfaktor 45'000 700 6'400'000'000 530 1'900 13'000'000

Iterationstiefe 1'000 1'000 10'000 1'000 4'000 60'000

Im letzten Bild, einer Mandelbrot-3D-Grafik, wurde die Anzahl der Schritte nicht nur durch einen Farbindex, sondern auch durch die Höhe des Punkts dargestellt. So entsteht ein "unendlich hohes Gebirge", wobei jedoch alle Spitzen, die größer als 100 sind, eingeebnet wurden.